This doesn't.
Sunday, November 8, 2009
Sunday, November 1, 2009
Dvorak, Everyman and the Devil's eve
The Macintosh uses an experimental pointing device called a ‘mouse’. There is no evidence that people want to use these things. I dont want one of these new fangled devices.
San Francisco Examiner, John C. Dvorak, 19 February 1984
A completely different Dvorak came up with a completely different input device for computers, which I'm experimenting with now. For now, it's slow going, but I'm picking up speed exponentially.
I just finished Everyman, by Philip Roth, and my god was it good. More about that later, when I can type faster.
And I seemed to have picked up a north American habit of carving pumpkins on the devil's eve.
At first we're good mates and all chummy...

but by the next day relations had become sour,
Is it just me, or does he even look a little sadder?
Tuesday, October 20, 2009
Time travel: it's happening.
I've decided I'm going to utilise my current research to travel into the future; to be precise, the weekend. It will take some time, perhaps a few days to complete the process, but at the end of it, I will no longer be in the present: I will be .... in the future!
Keep an eye out for me. I'll be wearing odd-looking clothes from the past, they'll seem very old. Perhaps I'll be able to pull them off as retro.
And who knows, if all goes well, by this time next week I'll be well on my way to next Wednesday.
Monday, October 12, 2009
Another array of additions.
More photos. I'm really warming up to Federation Square. It's an eclectic mish-mash of ideas, much like the National Australian Museum. And much like the idea of federation, I think. And it has free wireless and a great bar to take in the view of the `mighty' Yarra of the evening.



Then there are the random installations of street art. Like this one out front of the State Library of Victoria, right where I usually park my bike.

Then there's the wide array of fresh and exceptionally cheap sea-food.

Wednesday, September 23, 2009
Dammit, trumped by Frenchies again!
I've been playing a game with a friend of mine; swapping film clips on YouTube.
I thought I'd won when I shared up this little beauty, but she trumped me dragging up this eclectic visual tune.
What a *@#$%.
Tuesday, September 22, 2009
Up to your arses in maths jokes...
"Isn't statistics wonderful?"
"How so?"
"Well, according to statistics, there are 42 million alligator eggs laid every year. Of those, only about half get hatched. Of those that hatch, three fourths of them get eaten by predators in the first 36 days. And of the rest, only 5 percent get to be a year old for one reason or another. Isn't statistics wonderful?"
"What's so wonderful about all that?"
"If it weren't for statistics, we'd be up to our asses in alligators!"
"How so?"
"Well, according to statistics, there are 42 million alligator eggs laid every year. Of those, only about half get hatched. Of those that hatch, three fourths of them get eaten by predators in the first 36 days. And of the rest, only 5 percent get to be a year old for one reason or another. Isn't statistics wonderful?"
"What's so wonderful about all that?"
"If it weren't for statistics, we'd be up to our asses in alligators!"
Sunday, September 6, 2009
Some things I like
These days I get more than a little excited about small design details, whether it be computer/web, cinema or purchasable stuff.
I also recall some really good films I've seen; Samson and Deliah, and District 9. I should write down what I though. I just finished John Irvings The Hotel New Hampshire, which was almost as addictive as some of the T.V. series I've recently seen, like The Wire, Pushing Daisies, and The Lost Room. Although that last one may require a little explaining.

That all being said, yet not fleshed out, I merely add some photos, and will now bow out.

Thursday, August 27, 2009
I is back.
I'm back.
And to start things off, I'd like to put up a little picture I took today of a gorgeous building.
I've been seeing a lot of them around recently. They've started to capture my eye more and more often. Regularly my eye is draw up, above the heads of the on-lookers, and towards the towering structures that surround us every day. We live in them. We work in them. We turn to them for shelter, warmth, relief from heat (I hate the word "coolth"), an escape from everything. The Gruen transfer, Le Corbusier, home.... we all relate to buildings.




And so here's my first instalment of what will no doubt become a long series of building pictures. I call this one "Watch out Church, there's something sinister growing inside you"

Ok, perhaps I show a few more shots of the same building. It's times like this that I wish I had some of those great CanBerran artsy folk around, to get some good feedback on my pictures, composition, etc. Criticism, please! Constructive or not.
This was what I saw as I was riding up the street in East Melbourne. I was thinking "wow, the front of that church looks flimsy".

And then I decided to try and frame the building with the beautifully stark trees surrounding it, without success.

And when I finally got past it, I fell in love with the ominous talk dark structure inside, and how it reflects, or mocks, the pastel exterior. And I tried to get the cute lamp in the picture. Sharp eyes might catch a glimpse of the MCG at the end of the street.

If you want to know about the building I'm living in, just Google "Frank Cassar".
Adios.
Friday, May 8, 2009
Tuesday, March 24, 2009
Quick up-date
There's this guy who started to take photos using a CT scanner, which made for an interesting article in the New York Times and a nice slide-show. My favourite slide had the caption
"... and it is apparent from the placement of pickles, sauce and lettuce that the chef was under pressure.''I also read an amazing piece, about the demise of the newspaper industry and the resulting journalism. It's fantastic, and if anyone is reading this blog, I fully recommend them reading this article.
Saturday, January 10, 2009
The Real Line
All the numbers we are used to (and some numbers that we just don't care about too much) are really quite interesting. They have heaps of interesting properties that mathematicians like to talk about. And when they want to talk about all the numbers, they usually start by saying Consider the real line... . The real line is a representation of all those numbers, all placed on a straight line. (The reason why they're described as real is because there's another bunch of numbers called imaginary numbers, and they have even more interesting properties. But I'll talk about them another time.)
So here's a picture of the real line.
 I added a 3 just because it's cute, and also because 3 is a number, and numbers are on the real line. There's a little vertical line below the 3 to show us which point on the line is for the 3. Nice.
I added a 3 just because it's cute, and also because 3 is a number, and numbers are on the real line. There's a little vertical line below the 3 to show us which point on the line is for the 3. Nice.
The is there to remind us it's the real line. Though lord knows why. It's pretty bloody obvious, right? However, I'm not one to rock the establishment, so there it is,
is there to remind us it's the real line. Though lord knows why. It's pretty bloody obvious, right? However, I'm not one to rock the establishment, so there it is,  and all. (if we wanted to talk about imaginary numbers, we'd draw the line vertically and put an
and all. (if we wanted to talk about imaginary numbers, we'd draw the line vertically and put an  on it. Not so strange, eh?)
on it. Not so strange, eh?)
It's a representation of the real thing, of course, as the real (or actual) real line goes off to infinity to the right. And to the left, it goes past 0 down to negative infinity. Like this.

Ok, so I just added the symbols for 0 and plus and minus infinity. But they remind us that the real line goes on forever, in both directions.
What's interesting is that I've left the 3 there to show that all the number are represented on the real line. Here the number 3 is just a point, but what's also there is the number 3.5 (which is to the right of 3), the number 2.5, the number 3.14, etc.
In fact, if you think about it a little bit more, there's an infinite number of numbers just around 3. There's 2.5, 2.6, 2.7, 2.75, 2.9, 2.99, 2.9999, 2.99999999, etc. They're all there.
So, what if we're talking about all the numbers less than 3? Well, I'm going to colour them in with red, so that the line would look like.

That's it, there are all the points less than 3. In the bit that's red. Notice how I haven't included the little vertical line for the 3? It's not red because 3 is not one of the numbers less than 3. So I didn't colour it red.
Now what if the mathematician doesn't have a red pen? Well, they'd mark it out using little curvy lines. Like this.
 Since we don't include 3, we use a curvy line, kinda like a cap, that includes everything to the left. Hence all the numbers less than 3.
Since we don't include 3, we use a curvy line, kinda like a cap, that includes everything to the left. Hence all the numbers less than 3.
If we wanted to include the number 3 (if we were considering, say, all the number less than or equal to the number 3), we'd use some square brackets, like this.

Now we've got a handle on the square and curvy brackets on the real line, let's do something neat with them. Let's try and stake out all the numbers that are less than 3, but also greater than or equal to 1? How would you draw this? Yup, that's right, like this.

Finally, let's draw on the ideas I discussed in the last post on sets. How could we describe all the numbers less than 3 using sets? Easy. We'd say this.

Now A is represented by the red bit above four pictures ago. If we wanted to talk about all of the numbers greater than or equal to 1, but less than 3, as in the last picture, we'd simply refer to them like this.

Notice how I gave it a new label B?
Clever.
So here's a picture of the real line.
 I added a 3 just because it's cute, and also because 3 is a number, and numbers are on the real line. There's a little vertical line below the 3 to show us which point on the line is for the 3. Nice.
I added a 3 just because it's cute, and also because 3 is a number, and numbers are on the real line. There's a little vertical line below the 3 to show us which point on the line is for the 3. Nice.The
It's a representation of the real thing, of course, as the real (or actual) real line goes off to infinity to the right. And to the left, it goes past 0 down to negative infinity. Like this.

What's interesting is that I've left the 3 there to show that all the number are represented on the real line. Here the number 3 is just a point, but what's also there is the number 3.5 (which is to the right of 3), the number 2.5, the number 3.14, etc.
In fact, if you think about it a little bit more, there's an infinite number of numbers just around 3. There's 2.5, 2.6, 2.7, 2.75, 2.9, 2.99, 2.9999, 2.99999999, etc. They're all there.
So, what if we're talking about all the numbers less than 3? Well, I'm going to colour them in with red, so that the line would look like.

Now what if the mathematician doesn't have a red pen? Well, they'd mark it out using little curvy lines. Like this.
 Since we don't include 3, we use a curvy line, kinda like a cap, that includes everything to the left. Hence all the numbers less than 3.
Since we don't include 3, we use a curvy line, kinda like a cap, that includes everything to the left. Hence all the numbers less than 3.If we wanted to include the number 3 (if we were considering, say, all the number less than or equal to the number 3), we'd use some square brackets, like this.

Now we've got a handle on the square and curvy brackets on the real line, let's do something neat with them. Let's try and stake out all the numbers that are less than 3, but also greater than or equal to 1? How would you draw this? Yup, that's right, like this.

Finally, let's draw on the ideas I discussed in the last post on sets. How could we describe all the numbers less than 3 using sets? Easy. We'd say this.
Now A is represented by the red bit above four pictures ago. If we wanted to talk about all of the numbers greater than or equal to 1, but less than 3, as in the last picture, we'd simply refer to them like this.
Notice how I gave it a new label B?
Clever.
Sunday, January 4, 2009
Sets
A set is a collection of things. That's right, it's that simple. What those things are, depends on what you're talking about. For example, you can have a set of fractions, or a set of numbers, or a set of integrals, or a set of whatever (Sometimes mathematicians try to be cool and talk about a set of unicorns, or pink elephants, but that's just stupid.)
Sets are denoted by a set of curly brackets, like this: { }. And you put the things in your set inside the brackets, so that a set of two fractions would look like this.

Sometimes you might want to give it a name, (but not an imaginative one, because we're mathematicians) like A, so that you would write

That's all fine and dandy if you can write down the list of things you want to put in you set. But what if you want to talk about a whole bunch of things, where's there's a lot of them. Say an infinite number of them. Like, all the fractions between 1 and 3. Obviously there 3/2, and 4/5, and 8/3. But there's a whole lot of them. How can we describe such a set?
Well, we write down inside the curly brackets the rules for what's in the set and what's not. (This is excitingly close to the important concept of the Axiom of Choice (what a great name; "The Axiom Of Choice"), but I'm not going to talk about it, because I'm not an expert, and it deserves it's own blog, as it was the sort of idea and revelation that shook the very foundations of mathematics. (If we really want to know, it's about whether you can even talk about an infinite number of objects or not. Or something like that))
So, getting back to it, we write down a rule for what's in the set, and hope that someone else knows what we're talking about it. For example, we might want to talk about all of the numbers between 1 and 3 (There should be an infinite number of them, so we'd better make a rule!). We would write this like

One would read this out loud (if one was a mathematician) as
 is the set of all fractions, you'd write
is the set of all fractions, you'd write

where, as you can probably guess, the symbol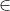 means `is one of', or in maths speak, `is in'. In other words
means `is one of', or in maths speak, `is in'. In other words
Sets are denoted by a set of curly brackets, like this: { }. And you put the things in your set inside the brackets, so that a set of two fractions would look like this.
Sometimes you might want to give it a name, (but not an imaginative one, because we're mathematicians) like A, so that you would write
That's all fine and dandy if you can write down the list of things you want to put in you set. But what if you want to talk about a whole bunch of things, where's there's a lot of them. Say an infinite number of them. Like, all the fractions between 1 and 3. Obviously there 3/2, and 4/5, and 8/3. But there's a whole lot of them. How can we describe such a set?
Well, we write down inside the curly brackets the rules for what's in the set and what's not. (This is excitingly close to the important concept of the Axiom of Choice (what a great name; "The Axiom Of Choice"), but I'm not going to talk about it, because I'm not an expert, and it deserves it's own blog, as it was the sort of idea and revelation that shook the very foundations of mathematics. (If we really want to know, it's about whether you can even talk about an infinite number of objects or not. Or something like that))
So, getting back to it, we write down a rule for what's in the set, and hope that someone else knows what we're talking about it. For example, we might want to talk about all of the numbers between 1 and 3 (There should be an infinite number of them, so we'd better make a rule!). We would write this like
One would read this out loud (if one was a mathematician) as
A is the set of all things which are bigger than 1 and less than 3.The colon is useful there when you want to be more specific about what sort of objects you're applying the rule to. For example, if you wanted to talk about all the fractions between 1 and 3, where
where, as you can probably guess, the symbol
A is the set of all numbers that are fractions () and are bigger than 1 and less than 3 (
).
Friday, January 2, 2009
More to come.
I never saw `Puppetry of the Penis', and heard some good things. Here's the next wave. Not for the faint of heart. ;)
There's going to be a maths blog later this afternoon.
There's going to be a maths blog later this afternoon.
Thursday, January 1, 2009
some maths terminology
So, as I head off to sleep for the first time in this new year, I leave you with these thoughts.
"There are things. Things do stuff, and stuff can be done to things.Here endth the stuff.
If I become more specific about these `things' and `stuff', do I sacrifice generality or introduce structure?"
Subscribe to:
Posts (Atom)






